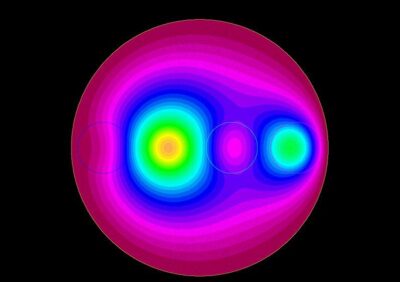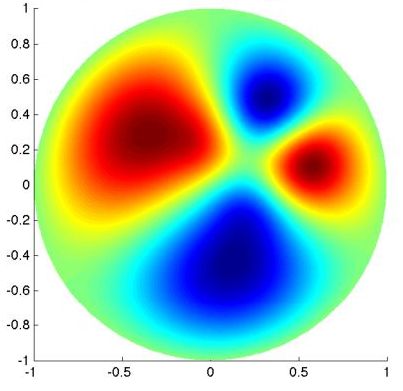
 What are the most relevant dimensionless parameters for transfer? Is there some asymptotic limit, over them, for which some simplified scaling can be obtained for transfer? Are there some optimal transfer configurations?
What are the most relevant dimensionless parameters for transfer? Is there some asymptotic limit, over them, for which some simplified scaling can be obtained for transfer? Are there some optimal transfer configurations?  Forced convection arises to improve heat and mass transfer in many contexts: heat exchangers, bio-heat transfer and tissue flux balance, chemical reactors, building and house cooling, vapor generators, etc. In forced convection, when fluid convection predominates over diffusion, the exchange between the fluid and the solid nevertheless strongly depends on diffusion because it is responsible for a transfer bottleneck within the solid (associated with thermal boundary layers). Hence, transfer issues are always configuration dependent, and cannot be improved by increasing convection only. Improving transfer thus necessitates more complete configuration exploration and parametric studies.
Forced convection arises to improve heat and mass transfer in many contexts: heat exchangers, bio-heat transfer and tissue flux balance, chemical reactors, building and house cooling, vapor generators, etc. In forced convection, when fluid convection predominates over diffusion, the exchange between the fluid and the solid nevertheless strongly depends on diffusion because it is responsible for a transfer bottleneck within the solid (associated with thermal boundary layers). Hence, transfer issues are always configuration dependent, and cannot be improved by increasing convection only. Improving transfer thus necessitates more complete configuration exploration and parametric studies.
 In the case of unidirectional convection, we generalized Graetz mode decomposition and provide the mathematical background for building quasi-analytical solutions of longitudinal exponentially decaying solutions along the flow direction (Pierre et al, 2020; Pierre et al, 2014; Ferhenbach et al, 2012; Bouyssier et al, 2013). These solutions for 3D problems lead us to propose some optimal configuration strategies (De Gournay et al, 2014). We used these generalized Graetz modes to analyze law Biot number limit of countercurrent exchangers (Dichamp et al, 2019). We also analyzed optimal density for various relative counter-convection in tube arrays (Dichamp et al, 2019).
In the case of unidirectional convection, we generalized Graetz mode decomposition and provide the mathematical background for building quasi-analytical solutions of longitudinal exponentially decaying solutions along the flow direction (Pierre et al, 2020; Pierre et al, 2014; Ferhenbach et al, 2012; Bouyssier et al, 2013). These solutions for 3D problems lead us to propose some optimal configuration strategies (De Gournay et al, 2014). We used these generalized Graetz modes to analyze law Biot number limit of countercurrent exchangers (Dichamp et al, 2019). We also analyzed optimal density for various relative counter-convection in tube arrays (Dichamp et al, 2019).
 We currently study vapor generators, planar exchangers and the thermal coupling between various channels.
We currently study vapor generators, planar exchangers and the thermal coupling between various channels. Air finger in a narrow opening generating periodic bubbles.
Publications
2024
Rudkiewicz, Martin; Gerald, Debenest; Plouraboué, Franck; David, Franck
Unidimensional forced convection generalized Graetz solutions Journal Article
In: SoftwareX, vol. 27, 2024.
@article{Rudkiewicz2024,
title = {Unidimensional forced convection generalized Graetz solutions},
author = {Rudkiewicz, Martin and Gerald, Debenest and Plouraboué, Franck and David, Franck},
doi = {10.1016/j.softx.2024.101834},
year = {2024},
date = {2024-08-01},
urldate = {2024-08-01},
journal = {SoftwareX},
volume = {27},
abstract = {Heat exchangers are essential in daily life and industries, but evolving demands, like miniaturization and electrification, challenge traditional designs. The Generalized Graetz Decomposition method offers a powerful solution, capable of efficiently modeling heat exchangers, even under these new conditions. Unlike conventional approaches, it generates analytical expressions that require minimal meshing, reducing computational costs. It accounts for all diffusion components, facilitating realistic modeling of low-velocity flows. This method provides a versatile tool for various boundary conditions. The software based on this method simplifies heatexchanger analysis, enables parametric studies, and has the potential to help heat exchanger design, impactingboth research and industry.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Rudkiewicz, Martin; Gerald, Debenest; Plouraboué, Franck; David, Franck
Unidimensionnal Forced Convection Generalized Graetz Solutions Journal Article
In: SoftwareX, vol. 27, 2024.
@article{Rudkiewicz2024b,
title = {Unidimensionnal Forced Convection Generalized Graetz Solutions},
author = {Rudkiewicz, Martin and Gerald, Debenest and Plouraboué, Franck and David, Franck},
doi = {10.1016/j.softx.2024.101834},
year = {2024},
date = {2024-01-08},
urldate = {2024-01-01},
journal = {SoftwareX},
volume = {27},
abstract = {Heat exchangers are essential in daily life and industries, but evolving demands, like miniaturization and electrification, challenge traditional designs. The Generalized Graetz Decomposition method o ers a powerful solution, capable of efficiently modeling heat exchangers, even under these new conditions.Unlike conventional approaches, it generates analytical expressions that require minimal meshing, reducing computational costs. It accounts for all diffusion components, facilitating realistic modeling of low-velocity flows. This method provides a versatile tool for various boundary conditions.The software based on this method simplifies heat exchanger analysis, enables parametric studies, and has the potential to help heat exchanger design, impacting both research and industry.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Plouraboué, Franck; Rudkiewicz, M.; David, F.; Neau, H.; Gerald, Debenest
Natural convective loops heat transfer scaling analysis Journal Article
In: International Journal of Heat and Mass Transfer, vol. 218, 2024.
@article{Plouraboué2024bb,
title = {Natural convective loops heat transfer scaling analysis},
author = {Plouraboué, Franck and Rudkiewicz, M. and David, F. and Neau, H. and Gerald, Debenest},
doi = {10.1016/j.ijheatmasstransfer.2023.124743},
year = {2024},
date = {2024-01-02},
urldate = {2024-01-02},
journal = {International Journal of Heat and Mass Transfer},
volume = {218},
abstract = {Heat transfer arising in natural convective loops is analyzed numerically and theoretically. Combining 3D direct numerical simulations, unidirectional heat-transfer semi-analytical computations, scaling arguments and asymptotic analysis new universal scaling laws are proposed to account for dimensionless heat transfer behavior of natural convective loops. It is found that the Reynolds number Re resulting from the buoyancy driven rotating convection (as well as the Péclet number) scales as Grashof number Gr as
for imposed temperature boundary conditions and
for mixed imposed temperature/flux heating conditions. These scaling laws are successfully confronted with experimental measurements in both heating configurations. It is shown that these scaling result from boundary layers dominated transfers without noticeable influence of possibly complex 3D flow patterns found in the fluid flow. These simple scaling laws constitute a progress over previously existing correlations which have disregarded the effect of boundary layers, heating configurations as well as fluid to solid variable diffusivity/conductivity.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
for imposed temperature boundary conditions and
for mixed imposed temperature/flux heating conditions. These scaling laws are successfully confronted with experimental measurements in both heating configurations. It is shown that these scaling result from boundary layers dominated transfers without noticeable influence of possibly complex 3D flow patterns found in the fluid flow. These simple scaling laws constitute a progress over previously existing correlations which have disregarded the effect of boundary layers, heating configurations as well as fluid to solid variable diffusivity/conductivity.
Plouraboué, Franck; Rudkiewicz, Martin; David, Franck; Neau, Hervé; Gerald, Debenest
Natural Convective Loops Heat Transfer Scaling Analysis Journal Article
In: International Journal of Heat and Mass Transfer, vol. 218, 2024, ISSN: 0017-9310.
@article{Plouraboué2024b,
title = {Natural Convective Loops Heat Transfer Scaling Analysis},
author = {Plouraboué, Franck and Rudkiewicz, Martin and David, Franck and Neau, Hervé and Gerald, Debenest},
doi = {10.1016/j.ijheatmasstransfer.2023.124743},
issn = {0017-9310},
year = {2024},
date = {2024-01-01},
urldate = {2023-01-01},
journal = {International Journal of Heat and Mass Transfer},
volume = {218},
abstract = {Heat transfer arising in natural convective loops is analyzed. Combining 3D direct numerical simulations, unidirectional heat-transfer semi-analytical computations, scaling arguments and asymptotic analysis new universal scaling laws are proposed to account for dimensionless heat transfer behavior of natural convective loops. These scaling laws are successfully confronted with experimental measurements in various heating configurations. It is shown that the leading heat-transfer exchanges in natural convective loops are mainly dominated by boundary layers transfers, without noticeable influence of possibly complex 3D flow patterns found in the fluid flow. The proposed simple scaling laws constitute a progress over previously existing correlations which have disregarded the effect of boundary layers, heating configurations as well as fluid to solid variable diffusivity/conductivity.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2023
Jaberi, Amin; Gerald, Debenest; Plouraboué, Franck
Marangoni-driven spreading and receding of a volatile droplet on a liquid layer Journal Article
In: Physical Review Fluids, vol. 82, 2023.
@article{Jaberi2023,
title = {Marangoni-driven spreading and receding of a volatile droplet on a liquid layer},
author = {Jaberi, Amin and Gerald, Debenest and Plouraboué, Franck},
doi = {10.1103/PhysRevFluids.8.073601},
year = {2023},
date = {2023-07-01},
journal = {Physical Review Fluids},
volume = {82},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2022
Saidakov, V; Plouraboué, Franck; Kozlov, N.
Vibroconvective heat transfer in cylindrical container with oscillating elastic boundaries Journal Article
In: Journal of Physics: Conference Series, vol. 2317, pp. 012015, 2022.
@article{Saidakov2022,
title = {Vibroconvective heat transfer in cylindrical container with oscillating elastic boundaries},
author = {Saidakov, V and Plouraboué, Franck and Kozlov, N.},
year = {2022},
date = {2022-07-01},
urldate = {2022-07-01},
journal = {Journal of Physics: Conference Series},
volume = {2317},
pages = {012015},
abstract = {Heat transfer in a horizontal annular region filled with the viscous fluid is studied experimentally. The external boundary of the working volume is formed by an elastic silicone shell, while the internal one – by a cylindrical copper heater. The walls of the shell are brought into symmetric oscillatory motion by two linear servomotors. The temperature outside the external cylinder is maintained constant by pumping the thermally stabilized liquid. The experiments are conducted with the low heating power that corresponds to relatively low values of the Rayleigh number. This allows maintaining a regime, in which the forced, vibrational convection is the main mechanism of heat transfer. Theoretical analysis of the experimental results shows that the structure of the fluid flows is determined by the competition between the free, thermal convection and the forced one – the steady streaming generated by vibration. At sufficiently high intensity of oscillations, the forced convection dominates and leads to the increase of the heat transfer rate.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2020
Pierre, Charles; Plouraboué, Franck
Analytical properties of Graetz modes in parallel and concentric configurations Journal Article
In: Meccanica, vol. 55, pp. 1545–1559, 2020.
@article{oatao26478,
title = {Analytical properties of Graetz modes in parallel and concentric configurations},
author = {Charles Pierre and Franck Plouraboué},
url = {https://oatao.univ-toulouse.fr/26478/},
doi = {10.1007/s11012-020-01192-4},
year = {2020},
date = {2020-06-01},
journal = {Meccanica},
volume = {55},
pages = {1545--1559},
publisher = {Springer},
abstract = {The generalized Graetz problem refers to stationary convection-diffusion in uni-directional flows. In this contribution we demonstrate the analyticity of generalized Graetz solutions associated with layered domains: either cylindrical (possibly concentric) or parallel. Such configurations are considered as prototypes for heat exchangers devices and appear in numerous applications involving heat or mass transfer.
The established framework of Graetz modes allows to recast the 3D resolution of the heat transfer into a 2D or even 1D spectral problem. The associated eigen-functions (called Graetz modes) are obtained with the help of a sequence of closure functions that are recursively computed. The spectrum is given by the zeros of an explicit analytical series, the truncation of which allows to approximate the eigenvalues by solving a polynomial equation. Graetz mode computation is henceforth made explicit and can be performed using standard software of formal calculus. It permits a direct and mesh-less computation of the resulting solutions for a broad range of configurations.
Some solutions are illustrated to showcase the interest of mesh-less analytical derivation of the Graetz
solutions, useful to validate other numerical approaches.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
The established framework of Graetz modes allows to recast the 3D resolution of the heat transfer into a 2D or even 1D spectral problem. The associated eigen-functions (called Graetz modes) are obtained with the help of a sequence of closure functions that are recursively computed. The spectrum is given by the zeros of an explicit analytical series, the truncation of which allows to approximate the eigenvalues by solving a polynomial equation. Graetz mode computation is henceforth made explicit and can be performed using standard software of formal calculus. It permits a direct and mesh-less computation of the resulting solutions for a broad range of configurations.
Some solutions are illustrated to showcase the interest of mesh-less analytical derivation of the Graetz
solutions, useful to validate other numerical approaches.
2019
Dichamp, Jules; Gournay, Frédéric De; Plouraboué, Franck
Thermal significance and optimal transfer in vessels bundles is influenced by vascular density Journal Article
In: International Journal of Heat and Mass Transfer, vol. 138, pp. 1–10, 2019.
@article{oatao23686,
title = {Thermal significance and optimal transfer in vessels bundles is influenced by vascular density},
author = {Jules Dichamp and Frédéric De Gournay and Franck Plouraboué},
url = {https://oatao.univ-toulouse.fr/23686/},
doi = {10.1016/j.ijheatmasstransfer.2018.12.185},
year = {2019},
date = {2019-04-01},
journal = {International Journal of Heat and Mass Transfer},
volume = {138},
pages = {1--10},
publisher = {Elsevier},
abstract = {A semi-analytic method is used in order to systematically compute stationary 3-D coupled convection-diffusion in various parallel counter-current configurations and evaluate their thermal significance. This semi-analytic method permits a complete exploration of physiologically relevant parameter space associated with the bio-heat transfer of parallel vessels bundles. We analyze thermal significance with various previously proposed criteria. Optimal transfer configurations are found to depend on the vascular density and Péclet numbers. The relevance of these findings for bio-heat modeling in tissues is discussed.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2016
Polezhaev, Denis; Duru, Paul; Plouraboué, Franck
Enhanced evaporation from an oscillating liquid in a capillary tube Journal Article
In: International Journal of Heat and Mass Transfer, vol. 95, pp. 288–295, 2016.
@article{oatao14612,
title = {Enhanced evaporation from an oscillating liquid in a capillary tube},
author = {Denis Polezhaev and Paul Duru and Franck Plouraboué},
url = {http://www.sciencedirect.com/science/article/pii/S0017931015303112
https://oatao.univ-toulouse.fr/14612/},
doi = {10.1016/j.ijheatmasstransfer.2015.12.012},
year = {2016},
date = {2016-04-01},
urldate = {2016-04-01},
journal = {International Journal of Heat and Mass Transfer},
volume = {95},
pages = {288--295},
publisher = {Elsevier},
abstract = {Enhanced evaporation inside a capillary tube into which the liquid/gas meniscus oscillates is experimentally studied. It is found that the meniscus oscillation can markedly level-off the evaporation rate, while keeping an apparent diffusive behaviour. The apparent diffusive coefficient can reach a tenfold increase in the explored range of parameters. The dependence of the effect is studied by varying the capillary tube diameter, the frequency and the amplitude of the liquid oscillations. The parametric dependence of the apparent diffusive coefficient is well captured by the associated dimensionless Péclet number. A nice collapse of the experimental measurements consistent with a quadratic scaling with Péclet number is found.
Such scaling is suggested by previous theoretical and experimental analysis associated with a Taylor dispersion transport mechanism. Nevertheless the prefactor of those theory is found to under-predict the observed effect by a factor three. This deviation from Taylor's dispersion driven transport predictions is discussed.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Such scaling is suggested by previous theoretical and experimental analysis associated with a Taylor dispersion transport mechanism. Nevertheless the prefactor of those theory is found to under-predict the observed effect by a factor three. This deviation from Taylor’s dispersion driven transport predictions is discussed.
Dichamp, Jules; de Gournay, Frédéric; Plouraboué, Franck
Theoretical and numerical analysis of counter-flow parallel convective exchangers considering axial diffusion Journal Article
In: International Journal of Heat and Mass Transfer, vol. 107, pp. 154-167, 2016.
@article{oatao16621,
title = {Theoretical and numerical analysis of counter-flow parallel convective exchangers considering axial diffusion},
author = {Jules Dichamp and Frédéric de Gournay and Franck Plouraboué},
url = {https://oatao.univ-toulouse.fr/16621/
http://www.sciencedirect.com/science/article/pii/S0017931015317038},
doi = {10.1016/j.ijheatmasstransfer.2016.09.019},
year = {2016},
date = {2016-01-01},
urldate = {2016-01-01},
journal = {International Journal of Heat and Mass Transfer},
volume = {107},
pages = {154-167},
publisher = {Elsevier},
abstract = {We perform a systematic analysis of heat transfer in a counter-current three dimensional convective exchanger, when the inlet/outlet influence is fully taken into account. The analysis, carried out for constant fluid properties, considers the various influences of the fluid/solid conductivity, the imposed convection, inlet/outlet far-field conditions, and lateral boundary conditions. Using a generalized Graetz mode decomposition which permits to consider, both transverse and longitudinal diffusion influence in the exchanger as well as in the inlets/outlets, we put forward several salient generic features of convection/conduction heat transfer. In all cases we found an optimal Péclet number for the cold or hot effectiveness. Even if, as expected, the larger the Péclet the larger the Nusselt number, high transfer performances are found to be poorly efficient and/or to necessitate non-compact elongated exchangers. Performance degradation arising at high Péclet number are found to be related to a "convective leaks" taking place within outlets. A fully developed regime occurs at large Péclet and/or for long exchangers, which is fully determined by the first eigenvalue of the generalized Graetz mode decomposition, which is an extension of classical Graetz analysis. Numerical results are found consistent with a generalized linear relation between effectiveness and the number of heat transfer units asymptotically established in the convection dominated regime. This study opens new perspectives for micro-heat exchangers where moderate convection provides the best effectiveness and compactness. This contribution is also useful for giving reference solutions to counter-flow exchangers with realistic inlet/outlet boundary conditions.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2014
Pierre, Charles; Bouyssier, Julien; Gournay, Frédéric De; Plouraboué, Franck
Numerical computation of 3D heat transfer in complex parallel heat exchangers using generalized Graetz modes Journal Article
In: Journal of Computational Physics, vol. 268, pp. 84–105, 2014.
@article{oatao11164,
title = {Numerical computation of 3D heat transfer in complex parallel heat exchangers using generalized Graetz modes},
author = {Charles Pierre and Julien Bouyssier and Frédéric De Gournay and Franck Plouraboué},
url = {https://oatao.univ-toulouse.fr/11164/
http://www.sciencedirect.com/science/article/pii/S0021999114001636?via=ihub},
doi = {10.1016/j.jcp.2014.02.037},
year = {2014},
date = {2014-07-01},
urldate = {2014-07-01},
journal = {Journal of Computational Physics},
volume = {268},
pages = {84--105},
publisher = {Elsevier},
abstract = {We propose and develop a variational formulation dedicated to the simulation of parallel convective heat exchanger that handles possibly complex input/output conditions as well as connection between pipes. It is based on a spectral method that allows to re-cast three-dimensional heat exchangers into a two-dimensional eigenvalue problem, named the generalized Graetz problem. Our formulation handles either convective, adiabatic, or prescribed temperature at the entrance or at the exit of the exchanger. This formulation is robust to mode truncation, offering a huge reduction in computational cost, and providing insights into the most contributing structure to exchanges and transfer. Several examples of heat exchangers are analyzed, their numerical convergence is tested and the numerical efficiency of the approach is illustrated in the case of Poiseuille flow in tubes.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Gournay, Frédéric De; Fehrenbach, Jérôme; Plouraboué, Franck
Shape optimization for the generalized Graetz problem Journal Article
In: Structural and Multidisciplinary Optimization, 2014.
@article{oatao10965,
title = {Shape optimization for the generalized Graetz problem},
author = {Frédéric De Gournay and Jérôme Fehrenbach and Franck Plouraboué},
url = {https://oatao.univ-toulouse.fr/10965/
http://link.springer.com/article/10.1007/s00158-013-1032-4},
doi = {10.1007/s00158-013-1032-4},
year = {2014},
date = {2014-01-01},
urldate = {2014-01-01},
journal = {Structural and Multidisciplinary Optimization},
publisher = {Springer},
abstract = {We apply shape optimization tools to the generalized Graetz problem which is a convection-diffusion equation. The problem boils down to the optimization of generalized eigen values on a two phases domain. Shape sensitivity analysis is performed with respect to the evolution of the interface between the fluid and solid phase. In particular physical settings, counterexamples where there is no optimal domains are exhibited. Numerical examples of optimal domains with different physical parameters and constraints are presented. Two different numerical methods (level-set and mesh-morphing) are show-cased and compared.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2013
Bouyssier, Julien; Pierre, Charles; Plouraboué, Franck
Mathematical analysis of parallel convective exchangers with general lateral boundary conditions using generalized graetz modes Journal Article
In: Mathematical Models and Methods in Applied Sciences, pp. 1–39, 2013.
@article{oatao9357,
title = {Mathematical analysis of parallel convective exchangers with general lateral boundary conditions using generalized graetz modes},
author = {Julien Bouyssier and Charles Pierre and Franck Plouraboué},
url = {https://oatao.univ-toulouse.fr/9357/
http://www.worldscientific.com/worldscinet/m3as},
doi = {10.1142/S0218202513500620},
year = {2013},
date = {2013-08-01},
urldate = {2013-08-01},
journal = {Mathematical Models and Methods in Applied Sciences},
pages = {1--39},
publisher = {World Scientific Publishing},
abstract = {We propose a mathematical analysis of parallel convective exchangers for any general but longitudinally invariant domains. We analyze general Dirichlet or Neumann prescribed boundary conditions at the outer solid domain. Our study provides general mathematical expressions for the solution of convection/diffusion problems. Explicit form of generalized solutions along longitudinal coordinate are found from convoluting elementary base Graetz mode with the applied sources at the boundary. In the case of adiabatic zero flux counter-current configuration, we recover the longitudinally linearly varying solution associated with the zeroth eigenmode which can be considered as the fully developed behavior for heat-exchangers. We also provide general expression for the infinite asymptotic behavior of the solutions which depends on simple parameters such as total convective flux, outer domain perimeter and the applied boundary conditions. Practical considerations associated with the numerical precision of truncated mode decomposition is also analyzed in various configurations for illustrating the versatility of the formalism. Numerical quantities of interest are investigated, such as fluid/solid internal and external fluxes.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2012
Fehrenbach, Jérôme; Gournay, Frédéric De; Pierre, Charles; Plouraboué, Franck
The Generalized Graetz Problem in Finite Domains Journal Article
In: SIAM Journal on Applied Mathematics, vol. 72, no. 1, pp. 99–123, 2012.
@article{oatao6558,
title = {The Generalized Graetz Problem in Finite Domains},
author = {Jérôme Fehrenbach and Frédéric De Gournay and Charles Pierre and Franck Plouraboué},
url = {https://epubs.siam.org/doi/10.1137/11082542X
https://oatao.univ-toulouse.fr/6558/},
doi = {10.1137/11082542X},
year = {2012},
date = {2012-01-01},
urldate = {2012-01-01},
journal = {SIAM Journal on Applied Mathematics},
volume = {72},
number = {1},
pages = {99--123},
publisher = {Society for Industrial and Applied Mathematics},
abstract = {We consider the generalized Graetz problem associated with stationary convection-diffusion inside a domain having any regular three-dimensional translationally invariant section and finite or semi-infinite extent. Our framework encompasses any previous extended and conjugated Graetz generalizations and provides theoretical bases for computing the orthogonal set of generalized two-dimensional Graetz modes. The theoretical framework includes both heterogeneous and possibly anisotropic diffusion tensors. In the case of semi-infinite domains, the existence of a bounded solution is shown from the analysis of two-dimensional operator eigenvectors which form a basis of L2 . In the case of finite domains a similar basis can be exhibited, and the mode?s amplitudes can be obtained from the inversion of newly defined finite domain operator. Our analysis includes both the theoretical and practical issues associated with this finite domain operator inversion as well as its interpretation as a multireflection image method. Error estimates are provided when numerically truncating the spectrum to a finite number of modes. Numerical examples are validated for reference configurations and provided in nontrivial cases. Our methodology shows how to map the solution of stationary convection-diffusion problems in finite three-dimensional domains into a two-dimensional operator spectrum, which leads to a drastic reduction in computational cost.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2009
Pierre, Charles; Plouraboué, Franck
Numerical Analysis of a New Mixed Formulation for Eigenvalue Convection-Diffusion Problems Journal Article
In: SIAM Journal on Applied Mathematics, vol. 70, no. 3, pp. 658–676, 2009, (Thanks to SIAM editor. This publication is available at http://epubs.siam.org/siap/).
@article{oatao5463,
title = {Numerical Analysis of a New Mixed Formulation for Eigenvalue Convection-Diffusion Problems},
author = {Charles Pierre and Franck Plouraboué},
url = {https://oatao.univ-toulouse.fr/5463/},
doi = {10.1137/080736442},
year = {2009},
date = {2009-01-01},
journal = {SIAM Journal on Applied Mathematics},
volume = {70},
number = {3},
pages = {658--676},
publisher = {Society for Industrial and Applied Mathematics},
abstract = {A mixed formulation is proposed and analyzed mathematically for coupled convection-diffusion in heterogeneous medias. Transfer in solid parts driven by pure di?usion is coupled with convection-diffusion transfer in fluid parts. This study is carried out for translation-invariant geometries (general infinite cylinders) and unidirectional flows. This formulation brings to the fore a new convection-diffusion operator, the properties of which are mathematically studied: its symmetry is first shown using a suitable scalar product. It is proved to be self-adjoint with compact resolvent on a simple Hilbert space. Its spectrum is characterized as being composed of a double set of eigenvalues: one converging towards ?? and the other towards +?, thus resulting in a nonsectorial operator. The decomposition of the convection-di?usion problem into a generalized eigenvalue problem permits the reduction of the original three-dimensional problem into a two-dimensional one. Despite the operator being nonsectorial, a complete solution on the infinite cylinder, associated to a step change of the wall temperature at the origin, is exhibited with the help of the operator?s two sets of eigenvalues/eigenfunctions. On the computational point of view, a mixed variational formulation is naturally associated to the eigenvalue problem. Numerical illustrations are provided for axisymmetrical situations, the convergence of which is found to be consistent with the numerical discretization.},
note = {Thanks to SIAM editor. This publication is available at http://epubs.siam.org/siap/},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2007
Plouraboué, Franck; Pierre, Charles
Stationary convection-diffusion between two co-axial cylinders Journal Article
In: International Journal of Heat and Mass Transfer, vol. 50, no. 23-24, pp. 4901–4907, 2007.
@article{oatao5471,
title = {Stationary convection-diffusion between two co-axial cylinders},
author = {Franck Plouraboué and Charles Pierre},
url = {https://oatao.univ-toulouse.fr/5471/
http://www.sciencedirect.com/science/article/pii/S0017931007004772},
doi = {10.1016/j.ijheatmasstransfer.2007.06.037},
year = {2007},
date = {2007-01-01},
urldate = {2007-01-01},
journal = {International Journal of Heat and Mass Transfer},
volume = {50},
number = {23-24},
pages = {4901--4907},
publisher = {Elsevier},
abstract = {In this note, we examine the high Peclet number limit of the stationary extended Graetz problem for which two families of real and imaginary eigenvalues are associated, respectively, with a downstream convective relaxation and the upstream diffusive establishment. The asymptotic behavior of both families of eigenvalues is studied, in the limit of large Peclet number and thin wall, which bring to the fore a single parameter dependence, previously mentioned in the literature from numerical investigations [M.A. Cotton, J.D. Jackson, in: R.W. Lewis, K. Morgan (Eds.), Numerical Methods in Thermal Problems, vol. IV, Pineridge Press, Swansea, 1985, pp. 504-515]. The fully developed region is specifically studied thanks to the first eigenvalue dependence on the Peclet number, on the thermal conductivity coefficients and on the diameter ratio of the cylinders. The effective transport between the fluid and the solid is investigated through the
evaluation of the fully developed Nusselt number and experimental measurements.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
evaluation of the fully developed Nusselt number and experimental measurements.
2005
Pierre, Charles; Plouraboué, Franck; Quintard, Michel
Convergence of the Generalized Volume Averaging Method on a Convection-Diffusion Problem: A Spectral Perspective Journal Article
In: SIAM Journal on Applied Mathematics, vol. 66, no. 1, pp. 122–152, 2005.
@article{oatao5482,
title = {Convergence of the Generalized Volume Averaging Method on a Convection-Diffusion Problem: A Spectral Perspective},
author = {Charles Pierre and Franck Plouraboué and Michel Quintard},
url = {https://oatao.univ-toulouse.fr/5482/
https://epubs.siam.org/doi/10.1137/040610015},
doi = {10.1137/040610015},
year = {2005},
date = {2005-01-01},
urldate = {2005-01-01},
journal = {SIAM Journal on Applied Mathematics},
volume = {66},
number = {1},
pages = {122--152},
publisher = {Society for Industrial and Applied Mathematics},
abstract = {A mixed formulation is proposed and analyzed mathematically for coupled convection-diffusion in heterogeneous medias. Transfer in solid parts driven by pure diffusion is coupled with convection-diffusion transfer in fluid parts. This study is carried out for translation-invariant geometries (general infinite cylinders) and unidirectional flows. This formulation brings to the fore a new convection-diffusion operator, the properties of which are mathematically studied: its symmetry is first shown using a suitable scalar product. It is proved to be self-adjoint with compact resolvent on a simple Hilbert space. Its spectrum is characterized as being composed of a double set of eigenvalues: one converging towards -∞ and the other towards +∞, thus resulting in a nonsectorial operator. The decomposition of the convection-diffusion problem into a generalized eigenvalue problem permits the reduction of the original three-dimensional problem into a two-dimensional one. Despite the operator being nonsectorial, a complete solution on the in?nite cylinder, associated to a step change of the wall temperature at the origin, is exhibited with the help of the operator's two sets of eigenvalues/eigenfunctions. On the computational point of view, a mixed variational formulation is naturally associated to the eigenvalue problem. Numerical illustrations are provided for axisymmetrical situations, the convergence of which is found to be consistent with the numerical discretization.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2001
Bouyssier, Julien; Fehrenbach, Jérôme; Gournay, Frédéric De; Pierre, Charles; Plouraboué, Franck
Analyse de la convection-diffusion entre deux tubes parallèles plongés dans un domaine cylindrique Unpublished
2001.
@unpublished{oatao10538,
title = {Analyse de la convection-diffusion entre deux tubes parallèles plongés dans un domaine cylindrique},
author = {Julien Bouyssier and Jérôme Fehrenbach and Frédéric De Gournay and Charles Pierre and Franck Plouraboué},
url = {https://oatao.univ-toulouse.fr/10538/},
year = {2001},
date = {2001-01-01},
booktitle = {20`eme Congr`es Franccais de Mécanique (CFM 2011)},
pages = {1--6},
address = {Besanccon, FR},
abstract = {Nous étudions la convection-diffusion tridimensionnelle entre tubes parallèles par une formulation théorique bi-dimensionnelle précédemment proposée. L'implémentation de cette formulation bi-dimensionnelle par éléments finis permet de calculer une vaste classe de configurations physique, hydrodynamiques et géométriques. Nous nous attachons à l'étude du champ de température et de l'évolution des flux en fonction du nombre de Péclet Pe, l'écart entre les deux tubes d, le rayon des tubes r et les vitesses des écoulements au sein des tubes.},
keywords = {},
pubstate = {published},
tppubtype = {unpublished}
}